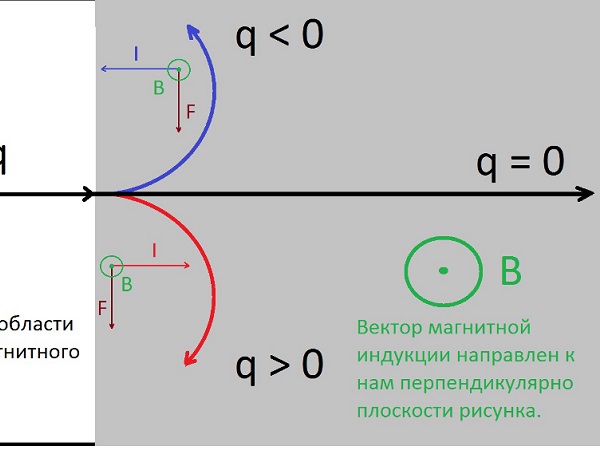
⭱

⭳

Сечение реакции

Эффективное поперечное сечение.

Или просто сечение, используется для выражения результатов опытов по столкновению частиц.

При условии однократного взаимодействия (тонкая мишень) и отсутствия взаимодействия между рассеивающими центрами, число N частиц, испытавших в единицу времени взаимодействие с ядрами мишени и изменивших траекторию (рассеявшихся), дается выражением

N = jnSLσ = jMσ (*)

Где j – плотность потока частиц (число частиц, упавшее в единицу времени на единицу поперечной площади (1 см2));

n – число частиц мишени в единице объема (1 см3);

S – облучаемая площадь мишени (см2);

L – толщина мишени (см);

M – полное число рассеивающих центров в облучаемой части мишени (см);

σ – величина, характеризующая вероятность взаимодействия и называемая поперечным эффективным сечением.

Рассмотрим куб со стороной 1 см. В нем находится n рассеивающих центров

N = jnσ

Для того чтобы лучше понять смысл σ предположим, что σ = 1 см2

Тогда N = jn – получается, что каждая падающая частица взаимодействует с каждым рассеивающим

центром. Т.о. из того, что

σ = 1 см2

следует, что рассеивающий центр перекрывает собой всю площадь мишени и пролететь мимо частицы не могут (а т.к. задачу мы рассматриваем в геометрическом смысле, то пролёты сквозь рассеивающий центр и означают взаимодействие).

Если взять теперь

σ = 0.5 см2 то N = 0.5 jn

т.е. налетающая частица взаимодействует уже только с половиной рассеивающих центров.

Т.о. смысл σ состоит в вероятности взаимодействия (численно равно ей, если выражать его в единицах элементарной площади) и при этом σ имеет размерность площади

Ядерные оболочки (уровни) Эффективное поперечное сечение
Деление ядер Распределение энергии деления между продуктами
Классификация частиц Классификация частиц от Максима Николаевича (внешняя ссылка)
Видеоматериалы История циклотрона за 1930 - 1980 года
Кафедра ядерной физики
История кафедры
Конспекты и учебные материалы
Статья в википедии
Контакты и сотрудничество:
Рекомендую наш хостинг beget.ru
Пишите на info@urn.su если Вы:
1. Хотите написать статью для нашего сайта или перевести статью на свой родной язык.
2. Хотите разместить на сайте рекламу, подходящуюю по тематике.
3. Реклама на моём сайте имеет максимальный уровень цензуры. Если Вы увидели рекламный блок недопустимый для просмотра детьми школьного возраста, вызывающий шок или вводящий в заблуждение - пожалуйста свяжитесь с нами по электронной почте
4. Нашли на сайте ошибку, неточности, баг и т.д. ... .......
5. Статьи можно расшарить в соцсетях, нажав на иконку сети: